Oppervlakte en omtrek van cirkels

Een belangrijke les in het rekenen is om te leren hoe je van een straal of diameter van een cirkel kan berekenen wat het oppervlakte of de omtrek is van de cirkel.

Voordat we gaan rekenen, moeten we eerst enkele termen begrijpen;



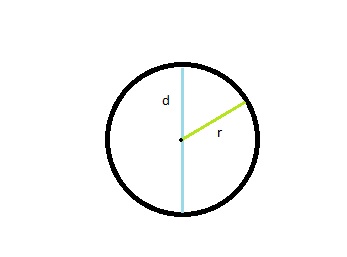
Allereerst de diameter (afkorting d). Dit is de lengte van de ene kant van de cirkel naar de andere kant van de cirkel. Het maakt niet uit waar je begint met meten, als je maar 1 punt op de cirkelrand neemt en dan recht naar de andere kant gaat (het verste punt van de cirkel).

Een tweede belangrijke definitie is de straal (afkorting r van radius). De straal is de helft van de diameter. Oftewel 2*r = d. De straal kan je meten door het middelpunt van de cirkel te pakken en dan naar de rand van de cirkel te meten in een rechte lijn. Het maakt niet uit waar je naar de rand van de cirkel gaat, want vanuit het midden is dat altijd gelijk.

Het is vaak makkelijker om de straal te meten en op basis daarvan de diameter te bepalen.

De laatste definitie die je moet kennen is Π (uitgesproken als pi). Pi heeft geen exacte waarden, maar dit is ongeveer 3,14159. Soms wordt het ook als 22/7 geschreven, al is dat niet helemaal juist.

Hoe bereken je het oppervlakte van een cirkel?
De formule om het oppervlakte te berekenen van een cirkel is Πr2 oftewel Π * r * r.

De eerste stap is dus om achter de straal (r) te komen. Die kan je meten, zoals we uitgelegd hebben of heb je gekregen. Stel dat r de waarde 8 heeft. Het oppervlakte is dan:

Oppervlakte cirkel = Π*r*r = 3,14*8*8 = 200,96.

Hoe bereken je de omtrek van een cirkel?
De formule om het oppervlakte te berekenen van een cirkel is 2Πr.

Net als bij het berekenen van de oppervlakte moet je eerst de straal weten. Stel dat de straal nu weer 8 is. De omtrek is dan:

Omtrek cirkel = 2*Π*r = 2*3,14*8 = 50.88.

Gebruiken mensen dit wel eens in hun werk?
Wij hebben een voorbeeld ontvangen van Wheelpoint over hoe het veranderen van de straal/diameter van banden en velgen (metalen binnenstuk van een band) een probleem kan vormen.

Sommige mensen vinden het mooier om een grotere band en velg op hun auto te hebben. Dat heeft echter een gevolg voor de snelheid die gemeten wordt.

Stel dat de diameter eerst 16 inch (straal is 8 inch) was en iemand wil nu 18 inch (straal is 9 inch), dan was de omtrek:

2*3.14*8 = 50.24

Nu is die

2*3.14*9 = 56.52

Hierdoor verandert de snelheid die de teller in de auto aangeeft. Als de auto 120km/u aangeeft, kan dit in het echt 124km/u zijn. Om dit zelf te hoeven berekenen zijn er rekenmachines voor zoals de bandencalculator van wheelpoint op https://www.wheelpoint.nl/banden. Een voorbeeld van een andere nuttige rekenopdracht die wat moeilijker is, is om je snelheid te berekenen https://nl.wikipedia.org/wiki/Snelheid.

Met dit voorbeeld willen we uitleggen dat rekenen niet alleen belangrijk is voor op school, maar dat het ook daarna als je werkt in verschillende situaties gebruikt wordt. Uit onderzoek blijkt dat leerlingen die wiskunde zien als waardevol en interessant vak, beter presteren.

Naar de website